How to Perform Matrix Operations and Linear Algebra in MATLAB
MATLAB, short for Matrix Laboratory, is a powerful tool widely used for matrix operations and linear algebra. Its rich set of functions and intuitive syntax make it ideal for engineers, scientists, and mathematicians. This article provides an in-depth guide to performing matrix operations and linear algebra in MATLAB, covering everything from basic matrix manipulations to more advanced concepts like eigenvalues and singular value decomposition.
Table of Contents
- Introduction to MATLAB for Matrix Operations and Linear Algebra
- Basic Matrix Operations
- Creating Matrices
- Matrix Addition and Subtraction
- Scalar Multiplication
- Matrix Multiplication
- Transpose of a Matrix
- Advanced Matrix Operations
- Inverse of a Matrix
- Determinant of a Matrix
- Trace of a Matrix
- Linear Algebra Concepts
- Solving Linear Systems
- Eigenvalues and Eigenvectors
- Singular Value Decomposition (SVD)
- Orthogonality and Orthonormality
- Special Matrices and Functions
- Identity Matrix
- Diagonal Matrix
- Zero and Ones Matrices
- Hilbert Matrix
- Practical Applications
- Principal Component Analysis (PCA)
- Least Squares Method
- Matrix Decompositions in Machine Learning
- Optimization and Performance Tips
- Conclusion
1. Introduction to MATLAB for Matrix Operations and Linear Algebra
MATLAB is designed for matrix manipulations and linear algebra computations. Its syntax and functions are optimized for these tasks, making complex mathematical operations straightforward and efficient. Understanding matrix operations and linear algebra is fundamental for various applications in engineering, physics, computer science, and data analysis.
2. Basic Matrix Operations
Creating Matrices
In MATLAB, matrices are created using square brackets, with elements separated by spaces or commas for rows and semicolons for columns.
% Creating a row vector
rowVector = [1, 2, 3];% Creating a column vector
columnVector = [1; 2; 3];
% Creating a matrix
matrix = [1, 2, 3; 4, 5, 6; 7, 8, 9];
Matrix Addition and Subtraction
Matrix addition and subtraction require matrices of the same dimensions. MATLAB performs these operations element-wise.
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
B = [9, 8, 7; 6, 5, 4; 3, 2, 1];% Matrix addition
C = A + B;
% Matrix subtraction
D = A - B;
Scalar Multiplication
Scalar multiplication involves multiplying each element of the matrix by a scalar value.
scalar = 2;
E = scalar * A;
Matrix Multiplication
Matrix multiplication follows the rules of linear algebra, where the number of columns in the first matrix must equal the number of rows in the second matrix.
F = A * B;
Transpose of a Matrix
The transpose of a matrix is obtained by swapping its rows and columns.
G = A';
3. Advanced Matrix Operations
Inverse of a Matrix
The inverse of a square matrix AA is the matrix A−1A^{-1} such that A⋅A−1=IA \cdot A^{-1} = I, where II is the identity matrix. Not all matrices have inverses; a matrix must be square and its determinant non-zero.
H = inv(A);
Determinant of a Matrix
The determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the matrix.
detA = det(A);
Trace of a Matrix
The trace of a matrix is the sum of its diagonal elements.
traceA = trace(A);
4. Linear Algebra Concepts
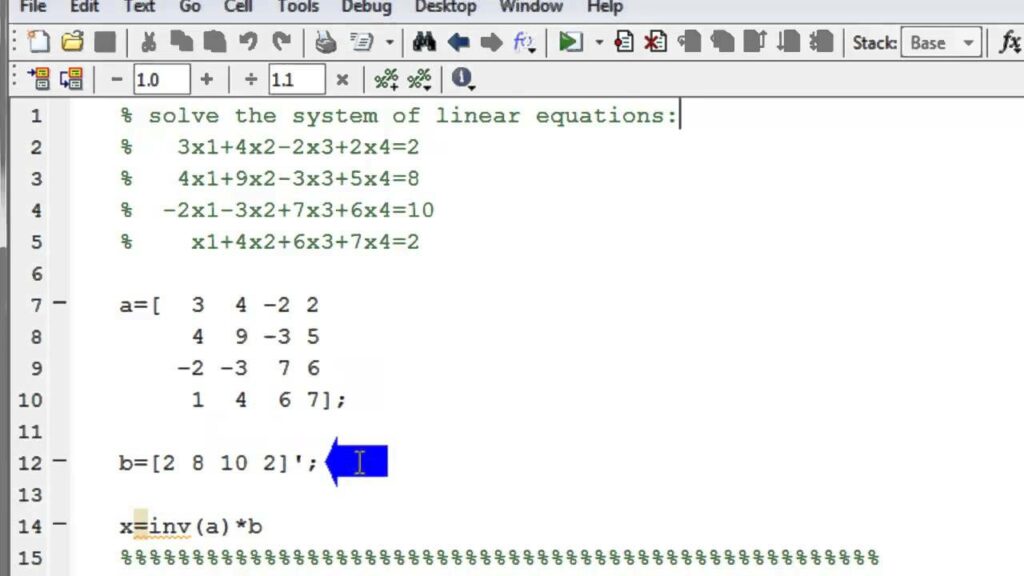
Solving Linear Systems
To solve a system of linear equations Ax=bAx = b, MATLAB provides the backslash operator (\), which is more efficient and numerically stable than computing the inverse.
A = [3, 2; 1, 2];
b = [2; 0];
x = A \ b;
Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are fundamental in linear algebra, providing insights into the properties of linear transformations.
[V, D] = eig(A);
Here, V contains the eigenvectors and D is a diagonal matrix with the eigenvalues on the diagonal.
Singular Value Decomposition (SVD)
SVD decomposes a matrix into three other matrices and is used in many applications, including signal processing and statistics.
[U, S, V] = svd(A);
Orthogonality and Orthonormality
Vectors are orthogonal if their dot product is zero. A set of vectors is orthonormal if they are all unit vectors and orthogonal to each other.
% Check orthogonality
dotProduct = dot(A(:,1), A(:,2));% Orthonormalize using QR decomposition
[Q, R] = qr(A);
5. Special Matrices and Functions
Identity Matrix
The identity matrix is a square matrix with ones on the diagonal and zeros elsewhere.
I = eye(3);
Diagonal Matrix
A diagonal matrix has non-zero elements only on the diagonal.
D = diag([1, 2, 3]);
Zero and Ones Matrices
Matrices filled with zeros or ones are useful in various computations.
Z = zeros(3, 3);
O = ones(3, 3);
Hilbert Matrix
The Hilbert matrix is a specific type of square matrix used in numerical analysis.
H = hilb(3);
6. Practical Applications
Principal Component Analysis (PCA)
PCA is used in data reduction and feature extraction, transforming data to a new coordinate system with orthogonal components.
data = rand(100, 3); % Sample data
coeff = pca(data);
Least Squares Method
The least squares method minimizes the sum of the squares of the residuals, providing the best fit for a set of observations.
A = [1, 1; 2, 1; 3, 1];
b = [1; 2; 2];
x = A \ b; % Least squares solution
Matrix Decompositions in Machine Learning
Matrix decompositions such as SVD and eigen decomposition are used in machine learning algorithms for dimensionality reduction and data compression.
% Using SVD for dimensionality reduction
[U, S, V] = svd(data);
reducedData = U(:, 1:2) * S(1:2, 1:2);
7. Optimization and Performance Tips
Efficiently performing matrix operations in MATLAB can significantly improve performance, especially with large datasets.
- Preallocation: Preallocate memory for matrices to avoid dynamically resizing them.matlab
A = zeros(1000, 1000);
- Vectorization: Use vectorized operations instead of loops.matlab
% Instead of using a loop
for i = 1:1000
A(i) = i^2;
end
% Use vectorized operations
A = (1:1000).^2;
- Built-in Functions: Use MATLAB’s built-in functions, which are optimized for performance.
- Sparse Matrices: Use sparse matrices for large matrices with many zero elements.matlab
S = sparse(A);
8. Conclusion
MATLAB is an indispensable tool for performing matrix operations and linear algebra. Its robust set of functions and efficient computation capabilities make it ideal for a wide range of applications in science, engineering, and data analysis. By mastering the basic and advanced operations covered in this article, you can leverage MATLAB’s full potential to solve complex mathematical problems and perform sophisticated data analyses.