How to Perform Basic Statistical Analysis in MATLAB
Statistical analysis is fundamental to data analysis, enabling us to understand and interpret data, draw conclusions, and make informed decisions. MATLAB, a high-performance language for technical computing, offers extensive tools for statistical analysis. This article provides an in-depth guide on how to perform basic statistical analysis in MATLAB, focusing on measures such as mean, median, and standard deviation. We’ll explore the mathematical foundations of these statistics, demonstrate how to calculate them using MATLAB, and discuss their interpretation and application in data analysis.
Table of Contents
- Introduction to Statistical Analysis in MATLAB
- Mean
- Definition and Importance
- Calculating Mean in MATLAB
- Interpreting Mean
- Median
- Definition and Importance
- Calculating Median in MATLAB
- Interpreting Median
- Standard Deviation
- Definition and Importance
- Calculating Standard Deviation in MATLAB
- Interpreting Standard Deviation
- Other Basic Statistical Measures
- Mode
- Variance
- Range
- Handling Data in MATLAB
- Importing Data
- Cleaning Data
- Best Practices in Statistical Analysis
- Conclusion
1. Introduction to Statistical Analysis in MATLAB
MATLAB is a versatile environment for data analysis, offering a broad range of functions for statistical calculations. These functions enable analysts and researchers to summarize data, identify patterns, and infer properties about a population from sample data. Basic statistical measures such as mean, median, and standard deviation are fundamental to this process and are widely used in various fields including engineering, finance, and social sciences.
2. Mean
Definition and Importance
The mean, or average, is a measure of central tendency that represents the sum of all data points divided by the number of points. It provides a single value that summarizes the data set, making it easier to understand the overall distribution.
Mathematically, the mean μ\mu of a data set x1,x2,…,xnx_1, x_2, …, x_n is defined as: μ=1n∑i=1nxi\mu = \frac{1}{n} \sum_{i=1}^{n} x_i
Calculating Mean in MATLAB
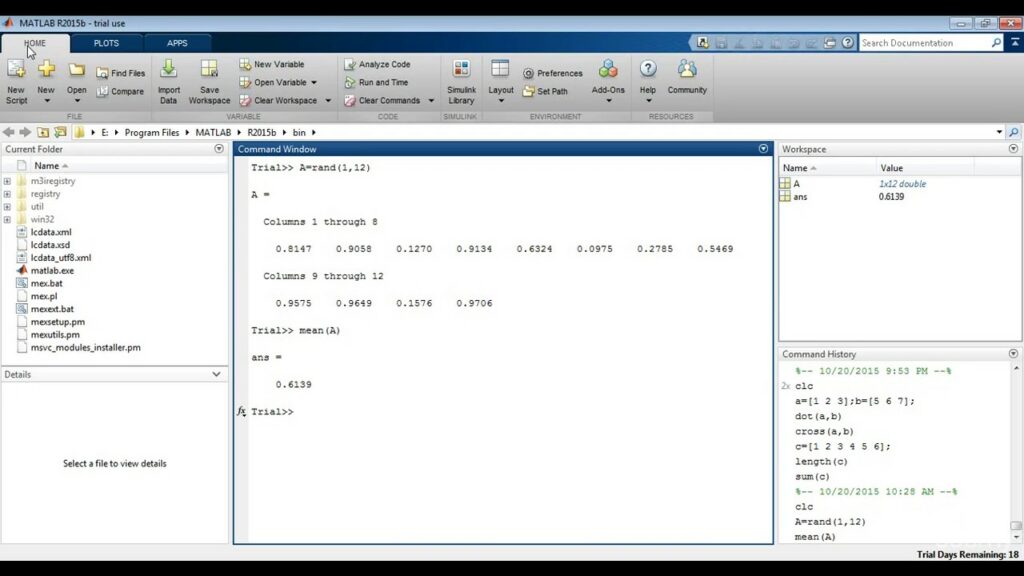
In MATLAB, calculating the mean is straightforward using the mean function. Here’s an example:
data = [1, 2, 3, 4, 5];
meanValue = mean(data);
disp(['Mean: ', num2str(meanValue)]);
This code snippet computes the mean of the data set [1, 2, 3, 4, 5].
Interpreting Mean
The mean is useful for understanding the central value of the data. However, it can be sensitive to outliers, which can skew the results. In such cases, the median may be a better measure of central tendency.
3. Median
Definition and Importance
The median is the middle value of a data set when it is ordered in ascending or descending order. If the number of data points is even, the median is the average of the two middle numbers. The median is less affected by outliers and skewed data than the mean, making it a robust measure of central tendency.
Calculating Median in MATLAB
MATLAB provides the median function to calculate the median of a data set:
data = [1, 2, 3, 4, 5];
medianValue = median(data);
disp(['Median: ', num2str(medianValue)]);
This calculates the median of the same data set [1, 2, 3, 4, 5].
Interpreting Median
The median provides a better measure of central tendency when the data contains outliers or is skewed. It is particularly useful in descriptive statistics to represent the typical value of a data set.
4. Standard Deviation
Definition and Importance
Standard deviation is a measure of the amount of variation or dispersion in a set of values. It quantifies how much the values deviate from the mean. A low standard deviation indicates that the values are close to the mean, while a high standard deviation indicates greater dispersion.
Mathematically, the standard deviation σ\sigma is defined as: σ=1n∑i=1n(xi−μ)2\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i – \mu)^2}
Calculating Standard Deviation in MATLAB
In MATLAB, the std function is used to calculate the standard deviation:
data = [1, 2, 3, 4, 5];
stdValue = std(data);
disp(['Standard Deviation: ', num2str(stdValue)]);
This computes the standard deviation for the data set [1, 2, 3, 4, 5].
Interpreting Standard Deviation
Standard deviation provides insight into the spread of the data. In fields such as finance, a higher standard deviation indicates higher risk or volatility. Understanding the dispersion of data points around the mean is crucial for statistical inference and hypothesis testing.
5. Other Basic Statistical Measures
Mode
The mode is the value that appears most frequently in a data set. It is useful for categorical data where the mean and median may not be meaningful.
data = [1, 2, 2, 3, 4, 4, 4, 5];
modeValue = mode(data);
disp(['Mode: ', num2str(modeValue)]);
Variance
Variance measures the spread of the data points around the mean. It is the square of the standard deviation.
data = [1, 2, 3, 4, 5];
varianceValue = var(data);
disp(['Variance: ', num2str(varianceValue)]);
Range
The range is the difference between the maximum and minimum values in a data set. It gives a sense of the data’s spread but is sensitive to outliers.
data = [1, 2, 3, 4, 5];
rangeValue = range(data);
disp(['Range: ', num2str(rangeValue)]);
6. Handling Data in MATLAB
Importing Data
MATLAB can import data from various sources including spreadsheets, text files, and databases. The readtable function is commonly used for importing data from spreadsheets:
data = readtable('data.xlsx');
Cleaning Data
Data cleaning involves handling missing values, removing duplicates, and correcting errors. MATLAB provides functions like rmmissing to remove missing data:
data = rmmissing(data);
7. Best Practices in Statistical Analysis
Understanding the Data
Before performing any statistical analysis, it is crucial to understand the data. This includes knowing the data types, identifying potential outliers, and understanding the context.
Choosing the Right Statistical Measure
Different measures provide different insights. Choose the appropriate statistical measure based on the data characteristics and the analysis objective.
Visualizing Data
Visualizing data helps in understanding patterns, trends, and anomalies. Use plots such as histograms, scatter plots, and box plots to complement statistical analysis.
Reporting Results
Present statistical results clearly and accurately. Include measures of central tendency and dispersion, and use visual aids to enhance understanding.
8. Conclusion
MATLAB is a powerful tool for performing basic statistical analysis, offering functions to compute measures such as mean, median, and standard deviation. Understanding these basic statistics is essential for analyzing data, drawing meaningful conclusions, and making informed decisions. By following best practices and leveraging MATLAB’s capabilities, you can effectively analyze and interpret your data.